Standardabweichung Rechner


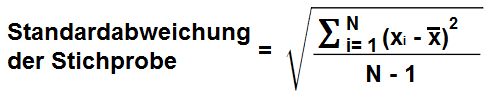
Standardabweichung der Bevölkerung
Der Standardabweichung rechner der Bevölkerung berechnet die Standardabweichung einer Population.
Eine Population repräsentiert den gesamten Datensatz. Dies schließt jede Person, jedes Element usw. ein. Wenn wir beispielsweise über eine Klasse von 30 Schülern sprechen, wäre die Bevölkerung alle 30 Schüler. Dies steht im Gegensatz zu einer Stichprobe (siehe unten), die einen Teil der Bevölkerung repräsentiert. Zum Beispiel kann eine Stichprobe 10 Schüler nehmen und ihre Daten untersuchen und eine Schlussfolgerung aus diesen 10 Schülern ziehen, um eine Schlussfolgerung darüber zu ziehen, wie die ganze Klasse tun wird.
Eine Standardabweichung ist ein statistisches Maß, das zeigt, wieviel Variation oder Dispersion es in einem Datensatz aus seinem Mittelwert gibt.
Eine niedrige Standardabweichung bedeutet, dass zwischen den einzelnen Datenwerten nicht viel vom Mittelwert der Gesamtmenge abweicht. Mit anderen Worten, die Datenpunkte neigen dazu, sehr nahe an dem Mittelwert zu liegen. Ein Beispiel für einen niedrigen Standardabweichungsdatensatz ist 2,21, 2,22, 2,23, 2,24, 2,25. Für diesen Datensatz ist der Mittelwert 2.23. Alle Datenwerte sind sehr nahe an diesem Wert.
Eine hohe Standardabweichung bedeutet, dass die Datenpunkte dazu neigen, über einen breiten Bereich von Werten verteilt zu werden; Mit anderen Worten, die einzelnen Datenpunkte sind weit von dem Mittelwert entfernt. Daher sind die Werte sehr weit voneinander entfernt. Beispielsweise haben die Daten 0, 100 einen Mittelwert von 50. Die einzelnen Datenpunkte liegen jedoch sehr weit von dem Mittelwert von 50. Dieser Datensatz weist eine sehr hohe Standardabweichung auf, so daß die Werte bis zu den Werten verteilt sind Mittelwert. Dieser Datensatz hat eine sehr hohe Standardabweichung, die Werte sind sehr weit vom Mittelwert entfernt.
Die Standardabweichung ist eine wichtige und hochver- wendete Maßnahme, da sie zeigt, wie sich die verteilten Daten von ihrem Mittelwert unterscheiden. Wenn wir die Standardabweichung berechnen, wissen wir, wie weit die Punktzahlen innerhalb eines Mittelwerts liegen. Daher können wir eine grobe Schätzung erhalten, wie nahe Werte innerhalb einer Standardabweichung liegen. Sagen wir zum Beispiel, dass der Mittelwert eines Tests 80 ist und die Standardabweichung 5 ist. Dies bedeutet, dass die Mehrzahl der Punkte zwischen 75 und 85 liegt, da die meisten Werte in einem Datensatz innerhalb einer Standardabweichung des Mittelwerts liegen. Und wenn wir bis zu 2 Standardabweichungen gehen würden, hätten fast alle Schüler zwischen diesem Wert gezählt. Nach der Chebyshev-Regel, die Standardabweichungen zusammenfasst, werden mindestens 75% der Gesamtbevölkerung innerhalb von 2 Standardabweichungen des Mittelwerts liegen. Mindestens 89% der Bevölkerung werden innerhalb von 3 Standardabweichungen eines Mittelwertes punkten. Und mindestens 93,75% einer Bevölkerung werden innerhalb von 4 Standardabweichungen eines Mittelwertes. So sagt uns die Standardabweichung statistisch sehr viel.
Um diesen rechner zu verwenden, gibt ein Benutzer einfach die Menge der Zahlen ein, für die er die Standardabweichung berechnen möchte, wobei jede Zahl durch ein Semikolon getrennt ist. Ein Semikolon muss verwendet werden, um die Werte zu trennen, sonst funktioniert der rechner nicht. Jedes andere Trennzeichen, einschließlich eines Leerzeichens zwischen den Zahlen, bewirkt, dass der rechner nicht funktioniert. Es werden nur Semikolons zu getrennten Werten erkannt. Nach Eingabe des Zahlensatzes klickt der Benutzer auf die Schaltfläche "Berechnen" und der resultierende Standardabweichungswert wird berechnet und angezeigt.
Die Einheiten, für die der Standardabweichungsrechner löst, sind die gleichen wie die Einheiten, die in das Eingabefeld eingegeben werden. Wenn zum Beispiel die in das Eingabefeld eingegebenen Werte in Zoll liegen, wird der resultierende Standardabweichungswert in Zoll liegen. Der rechner wechselt nicht von Eingang zu resultierendem Wert.
Die Berechnung der Standardabweichung ist für viele verschiedene statistische Zwecke wichtig und bietet eine weitere Möglichkeit, unsere Ergebnisse zu quantifizieren. Für die Elektronik, können wir einen durchschnittlichen Strom, Spannung, etc Wert haben. Mit der berechneten Standardabweichung können wir bestimmen, wie viele Standardabweichungen ein gegebener Strom, Spannung, etc. über seiner Norm liegt. Dies könnte für verschiedene mögliche statistische Zwecke nützlich sein.
Standardabweichung der Stichprobe
Der Standardabweichung der Stichprobe rechner berechnet die Standardabweichung für eine Stichprobe einer Population.
Eine Stichprobe einer Population repräsentiert einen Teil der Bevölkerung, der für statistische Zwecke gewählt wird, anstatt die gesamte Gesamtbevölkerung, die der Rechner oben ist.
Die Standardabweichung einer Population wird anders berechnet als die Gesamtbevölkerung. Anstelle der Teilung durch die ganze Zahl der Stichprobe, die wir normalerweise als N repräsentieren, um die volle Anzahl von Einheiten darzustellen, dividieren wir durch N-1. Dies stellt immer sicher, dass die Standardabweichung für eine Probe immer etwas höher als die Standardabweichung für die Population ist.
Das Dividieren durch N-1 mag wie eine seltsame Konvention erscheinen, aber da eine Probe nicht die volle Bevölkerung repräsentiert, verwenden Mathematiker N-1, um der Tatsache Rechnung zu tragen, dass die volle Population nicht verwendet wird. Also, die Probe wird etwas höher (es bump den Wert ein wenig).
Um diesen rechner genau wie der letzte zu verwenden, geben Sie einfach in die Liste der Nummern ein, für die Sie die Standardabweichung finden möchten, und klicken Sie dann auf die Schaltfläche "Berechnen". Die Standardabweichung der Zahlen wird automatisch berechnet und angezeigt.
Beispiele für Berechnungen
Berechnen der Standardabweichung der Zahlen 3, 5, 7, 9, 11 und 17.
Antwort:
Standardabweichung der Bevölkerung: 4,5338235029118
Standardabweichung der Stichprobe: 4,9665548085838: 7
Berechnen der Standardabweichung der Zahlen 1, 2, 3,5, 6,8, 9,7.
Antwort: Ähnliche Ressourcen
Signifikante Stellen Rechner
Standardabweichung der Bevölkerung: 2,2983085567918
Standardabweichung der Stichprobe: 2,8148416178061
Runden Signifikante Stellen Rechner
Wissenschaftliche Schreibweise Rechner
Faktorisierung Rechner
Konfidenzintervall Rechner
Hypothesentest Rechner
Tschebyscheff-Ungleichung Rechner
Bernoulli Ungleichung Rechner
Korrelationskoeffizient Rechner
Gleichungssystem Rechner
